Journal of Multimedia Theory and Applications (JMTA)

ISSN: 2368-5956

1. Introduction

Stereo matching is the process of finding corresponding points that represent the same object in different view images of the same scene. The distance between the coordinates of corresponding points in different views of images taken from different angles, namely disparity, could be used to compute the depth of the scene. Stereo matching, which is widely applied into three-dimensional modeling, motion capture and intelligent navigation for vehicles, is a key technique in stereo vision field. Simple as the principle of stereo matching is, it is still highly challenging to accurately computing the dense depth map, due to interferences in realistic scenes, such as the complex actual situation, severe occlusion, lighting variation and image noise.

The core work of stereo matching is to find the corresponding points representing the same object in left and right images. According to the difference in optimization methods, dense stereo matching can be classified into global method and local method. Global stereo matching correlates depth estimation of adjacent pixels together through introducing smooth constraints, and estimates the disparity of all pixels by solving a global objective function. While local stereo matching usually adopts a window-based approach to conduct searching and matching individually for each pixel.

Disparity maps of high precision can be gained by applying global optimization method, but due to its large number of parameters and high computation complexity, this method cannot be applied to systems with real-time requests.

In this paper, targeting the balance between algorithm's accuracy and execution time, we present a novel real-time stereo matching method. With an adaptive window based disparity refinement process, the proposed solution can achieve the accuracy equivalent of global method, and the method supports parallel processing so it can be used for real-time video applications.

The rest of the paper is organized as follows. Section 2 explains and cites related works that perform stereo matching. Section 3 describes the procedure of disparity estimation, including matching cost initialization and cost aggregation. Section 4 represents the details of disparity refinement, mainly focusing on occlusion detection and adaptive window construction. Section 5 shows the experimental results. Finally, we conclude with a brief summary in section 6.

2. Related Work

A stereo matching algorithm tries to solve the correspondence problem for projected scene points and the result is a disparity map. A good summary of many stereo matching algorithms can be found in Brown et al. and Scharstein and Szeliski, which summarize and categorize the two-view stereo matching method and its evaluation system in a comprehensive way. Classical global methods include graph cut (Boykov et al. 2001) and belief propagation (Scharstein et al. 2003). While adaptive weight (Yoon and Kweon 2006) and variable window (Zhang et al. 2009) are two classical methods of local stereo matching, which can ensure relatively high computation precision while significantly reducing computation complexity. Because it is unnecessary to take into account the correlation between adjacent pixels, the implementation of local method is relatively easier and efficient. However, this method calls for an assumption that the depth values of the pixels inside the window are the same, which, under many circumstances (especially in bounding areas where depths are not continuous), cannot be fulfilled; therefore, choosing the proper size for windows is the key point in this method. Too small matched windows will invalidate the smoothing effect and amplify depth noise; whereas too big windows will result in error matching in some fine structures and discontinuous areas.

Recently, in order to improve the effect of stereo matching on occlusion and uncharacteristic areas, some global-local hybrid methods (Hirschmüller 2008) and segmentation-based method (Bleyer et al. 2010) are proposed, further enhancing accuracy of disparity map on the premise of slightly increased amount of computation. However, because of the fact that dense stereo matching requires the separate calculation of disparity for each pixel in the images, sequential computing based on single processors can hardly meet the real-time requests.

The most up-to-date literature show that with the improvement of the performance of GPGPU (general purpose graphic processing unit), using parallel programming techniques like CUDA (compute unified device architecture) to improve and optimize stereo matching has become a research hotpot. A good summary of many stereo matching algorithms can be found in M. Humenberger et al. (2010), which gives a brief overview of the work related to embedded real-time stereo vision systems. A GPU-based system was introduced by Yang et al.. Using an SAD-based algorithm, they achieved a frame rate of 11.5 fps for an image size of 512 × 512 and 94 disparities on an ATI Radeon 9800 XT graphics card. Ernst and Hirschmueller (2008) proposed a semi-global matching approach (SGM) to overcome the drawbacks of local matching, and they implemented the algorithm on a Ge Force 8800 ULTRA GPU reaches a frame rate of 4.2 fps at 640 × 480 with 128 disparities and 13 fps at 320 × 240 with 64 disparities.

Gong et al. (2007) implemented parallel acceleration for 6 mainstream local stereo matching methods, and conducted a comparative analysis of their execution performances. Yu et al. (2010), on the basis of adaptive weight method, put forward an iterative aggregation method using exponential step-size adaptive weight (ESAW), and improved the algorithm's speed by nearly ten times through parallel optimization on GTX8800 graphic processing unit. Zhang et al. (2011) parallel optimized the variable window method, and proposed a fast bit-wised voting method to accelerate the post-processing procedure of the algorithm, enabling the algorithm to reach a speed of nearly 100fps when processing images with a resolution of 320x240. However, due to the dependence on data during the cost aggregation stage, in order to realize parallelization, the above methods always make a certain amount of trade-off on accuracy. In order to compensate for the accuracy loss of the algorithm during parallelization, Kowalczuk et al. (2013) presented a refinement method featuring iteration of horizontal and vertical similar to the aggregation stage to refine the initial disparity image, which effectively improves the accuracy of disparity map. But this method does not differentiate error points according to their types, so the estimation of disparity in occlusion areas is not quite satisfactory.

3. Disparity Estimation

3. 1. Matching cost initialization

Matching cost is the metric function to judge whether two pixels are similar, and it's the only foundation for estimation of disparity. Therefore a good matching cost function plays a very important role in improving the algorithm's robustness in different scenes. Hirschmüller and Scharstein (2009) have studied and evaluated the commonly used matching cost functions at present, and after numerous experiments, they found that the matching cost function based on Census non-parametric transformation (Zabih and Woodfill 1994) has the most balanced performance in all test collections, with a particularly good adaptability to intensity distortion caused by lighting variation. The main idea of Census transform is to build a p-centered window for a random pixel p, and generate a bit-string for each p according to formula (1):

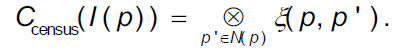
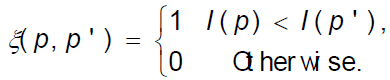
Here I(p) means luminance value of pixel p, and N(p) is the p-centered transforming window. Thus, the similarity measurement between the two pixels can be expressed by the distance between bit-string after Census transformation, namely, Hamming distance: the smaller Hamming distance is, the higher the matching degree of the two pixels is.

Census transform calculates matching cost according to the relationship of size between two pixels instead of relying directly on the values, so it possesses a better adaptability to range distortion. However, we find out that the following two problems will occur if using Census transform as the only matching cost:

1. Census transform has a lower pixel distinguishing degree for pixels in areas with simple textures and repeated structures. Because the specific pixel values are not considered, different pixels in these areas are likely to have the same Census transform values;
2. Census transform has a lower tolerance of image noise. Because Census transform is highly dependent on the central pixel, when noise points appear in the central pixel, the matching result is unpredictable. It is also mentioned by Hirschmüller and Scharstein (2009) that the matching results based on Census transform are not quite satisfactory in an environment of intense noise.

Aiming the above problems and considering that the commonly used AD cost function has better matching effects in areas with smooth textures, this paper adopts the matching cost function that combines AD and Census transform together. For a random pixel p in the left view, establish a p-centered 9x7 window and define the matching cost of p as follows:

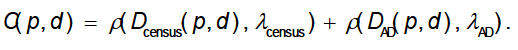
Here d is the presupposed disparity value, D_census and D_AD are the matching costs based on Census transform and AD respectively, ρ(D,λ) is a normalized function, with the following computing formula:

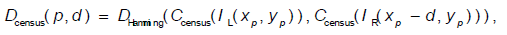
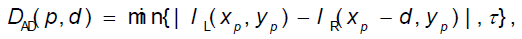
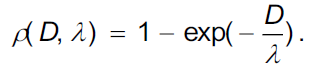
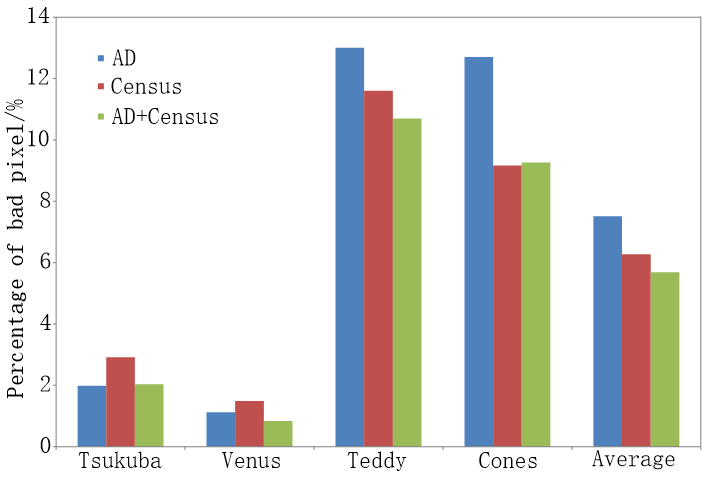
I_L(x,y) and I_R(x,y) refer to the gray values of corresponding pixels in left and right view respectively, C_census is calculated from Formula (1), λ_census, λ_AD and τ are prior parameters. Normalized function avoids the matching cost overly leaning to one certain type, and the λ is used for easily controlling the weights of the two matching cost, which enables the algorithm to combine well the advantages of Census and AD, and to have a better adaptability to intensity distortion and noise. Figure 1 demonstrates the stereo matching results using AD, Census and AD+Census as matching cost. It can be seen that in Tsukuba and Venus, the effect of AD is better than that of Census, but in Teddy and Cones, the effect of Census is better than that of AD. Nevertheless, AD+Census, combining the advantages of the two, performs the best under the four sequences with the lowest average error rate of all three methods.

3. 2. Iterative cost aggregation

The work following matching cost initialization is to estimate the disparity value of pixels according to the matching cost. Inspired by the idea of ESAW (Yu et al. 2010), this paper adopts the exponential step-size iterative aggregation method to estimate disparity. The basic thought of this algorithm is to construct a support window for each pixel, and then to use adaptive weight to aggregate the initial matching costs of the pixels in the window. It simplifies the original 2D aggregation into two 1D aggregations, namely horizontal and vertical aggregation, and uses an exponential iterative process to further reduced the time complexity. After calculating the final matching cost of central pixel under every hypothetic disparity value, we use the common WTA strategy to select disparity value with the smallest matching cost as the initial disparity value of center pixel.

Compared to the traditional adaptive weight method (Yoon and Kweon 2006), the iterative aggregation method is more suitable for parallel processing, but there exists a certain amount of loss of accuracy during computation, which is mainly reflected in the following two aspects:

1. The traditional adaptive weight method computes the weights both in target image and reference image during the stage of matching cost aggregation, but the parallel method usually computes just the pixel weight of the target image and abandons the weight of the reference image, as illustrated in formula (7). This is more suitable for parallel computation, but the matching cost after aggregation will have a lower distinguishing degree for different pixels.

(7)


2. In terms of weight calculation, exponential step-size iterative aggregation method discomposes the computation of a single weight into the result of many middle pixel weights' multiplication, as illustrated in formula (8). When there is a big difference between the middle pixel r_k and the two target pixels p,q, while the difference of target pixels themselves are relatively small, this computing method will cause a big error, and then lead to mismatch. This kind of mismatching is particularly prominent in the occlusion and edge area of the image.

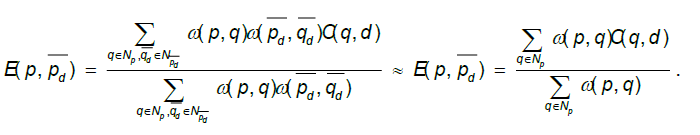
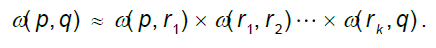
However, matching cost aggregation is the most time-consuming step in local stereo matching algorithm, so in this step it is necessary to exchange limited computation accuracy for a significant enhancement of execution time. This paper, in order to realize the algorithm's balance between execution time and accuracy, takes the strategy of exchanging accuracy for time in the stage of disparity estimation so as to improve the execution time of the algorithm; then takes a refinement step in post-processing stage to verify and update the initial disparity values, exchanging a small time cost for the improvement of computation accuracy.

4. Disparity Refinement

4. 1. Occlusion and mismatch detection

This paper proposes a disparity refinement method based on adaptive windows. First we conduct a consistency check on left and right disparity images according to formula (9). d_L and d_R in formula (9) represent left disparity image and right disparity image respectively. Inspired by the work of Hirschmüller (2008), this paper further classifies error points into occluded points and mismatched points. According to the geometrical principle of stereo vision, if the corresponding point of a certain pixel point in the left view cannot be found in the right view, then its corresponding epipolar line in the right view should have no intersection with the disparity value of the right view, otherwise if the point in the scene can be seen in both views, then there must be an intersection. Therefore, we can use this principle to judge whether the error point is caused by occlusion or mismatch.

For the error point p in the left image, define d_L(x,y_p) and d_R(x,y_p) as the disparity values of pixels in same the row of p in left and right views respectively, define p's corresponding epipolar line e(p,d) as a point set about d, as illustrated in formula (10). If d_R(x,y_p) and e(p,d) do not intersect, p should be perceived as the occluded point, otherwise, it should be perceived as the mismatched point.

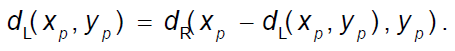
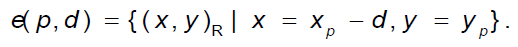
Figure 2 shows the results of using the above method to detect occlusion on Tsukuba's left view. In the figure, there are the original image, the results of this paper and the ground truth successively from left to right. In order that the result of right disparity image are also needed in occlusion tests, and there exist some errors in the right disparity image produced by proposed method, so there are some differences between the occlusion test result in this paper and the ground truth.

(a) Original image                       (b) Detected occlusion
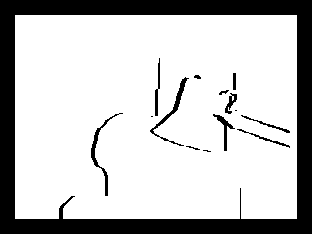(c) Ground truth

4. 2. Disparity refinement based on adaptive window

After classifying error points, different updating strategies can be adopted according to different error types. It can be known that the occluded point usually come from background pixels, therefore they can be updated by values with the minimum disparity in their adjacent background areas; while mismatched point usually occurs on object surfaces with complex textures, in either foreground or background, and the disparities in the adjacent areas do not vary too much, so these error points can be refined according to the statistical result of disparity values in adjacent areas. This paper proposes to build an adaptive window based on color similarity and Euclid distance for each error point. Theoretically, areas with similar colors should possess similar disparity values, the values of error points can be refined according to disparity statistics inside of the window. The construction process of adaptive windows is similar to original variable window (Zhang et al. 2009), for any random error point p, define a four-element set as illustrated in formula (11):

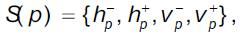
The elements in the four-element set form two orthogonal line segments in horizontal and vertical directions where p is located, as illustrated in formula(12).

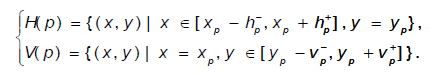
The length of these two segments can be decided under the constraints of color and distance in formula (13), where L1, L2, τ1 and τ2 are user defined parameters, and their relations should meet: L1>L2 and τ1>τ2.

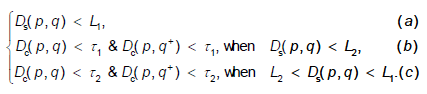
In formula (13), the parameter q+ means the adjacent pixel following q. Ds(p,q) represents the Euclid distance between p and q. Dc(p,q) is the color difference between p and q, which calculating as illustrated in formula(14).

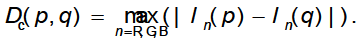
Being different from original variable window (Zhang et al. 2009), this paper improves the constraints. Formula (13a) set an upper limit value for the size of the window; formula (13b) regulate that not only the color difference between any random pixel q and p, but also the color difference between the q's following pixel and p must be less than a threshold, so that part of the interference of image noise can be excluded; while formula (13c) regulate that when the distance between q and p is more than L₂, a smaller threshold value is needed to further constrain the color difference between q and p, so as to better control the accuracy of the window size, making it possible to gain a relatively large window in areas where the color difference is small, and avoiding the window to be too small in areas with rich textures.

After establishing the foregoing orthogonal segments for each error point, all horizontal segments of the pixels on the vertical segment where p is located are combined together to form the p-centered adaptive window, as illustrated in formula (15).

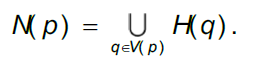
Figure 3 shows the result of the adaptive window for four pixel points in Teddy left view. It can be seen that the shape of the window can change arbitrarily, and the bounding area of the window is basically consistent with that of the color, whereas in areas with smaller color differences, the window can reach the preset maximum value.

After establishing the adaptive window, according to the previous analysis, the error points caused by occlusion could be updated by the minimum value of the reliable point in the window; and the error points caused by mismatch could be refined by the reliable point with the largest number inside the window. The concrete refinement method is illustrated in formula (16), where N*(p) stands for the set of reliable disparity points in the window centered in p; Ψ(d_q) is the statistical histogram of N*(p).

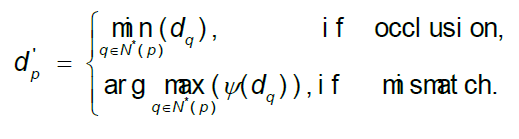
At last, this paper processes a 3x3 median filtering on the disparity image to further remove disparity noise. After that, the procedure of the algorithm is completed.

5. Experiment and Analysis

The proposed method has been parallel optimized, tested and evaluated on the nVIDIA GeForce GTS450 graphic card (192 CUDA cores and 1G graphic memory). Parameter settings involved in the optimization process are provided in Table 1. Other relevant parameters are set to the default value in reference paper.

Table 1. Parameter settings.

Parameters	λ census	λ AD	τ	L1	L2	τ1	τ2
Value	50	10	60	32	17	20	6

In terms of accuracy evaluating, this paper verifies the proposed method on the classic Middlebury benchmark: Tsukuba, Venus, Teddy and Cones. The results of disparity estimation are illustrated in figure 4, where the first column is the original image, the second is the ground truth, the third is the results of proposed method and the fourth column is the difference between the result of proposed method and the ground truth, in which the black area means the error on occlusion region and the gray area means the error on non-occlusion region. From the result of disparity estimation, it can be seen that the proposed method has more accurate result on the occlusion area, especially in Venus and Teddy, and the area with repeated textures (the net-like structure in the upper right) in Cones. But for the object's bounding area in Tsukuba and the bottom area of Teddy, the result of proposed method need further improvement.

(a) Original Image
(b) Ground Truth
(c) Proposed Result
(d) Errors

Submitting the third column of image in figure 4 to the Midllebury evaluation website, the quantitive results as shown in table 2 can be achieved. Table 2 displays the error pixels' proportion in all pixels, and the threshold value of error is 1, meaning that if the difference between computed disparity value and the standard value is bigger than 1, then it should be marked as an error. There are three types of errors all together, namely, nonocc: the error pixels' proportion in non-occlusion areas; all: the error pixels' proportion in all areas; and disc: the error pixels' proportion in discontinuous areas. Other algorithms involved in the comparison include: the effective SemiGlob method (SemiGlob), the classic adaptive weight method (AW), the method based on iterative disparity refinement (IterRefine), the method based on adaptive windows (VariableWnd) and the exponential step-size adaptive weight (ESAW). The latter three of them are real-time stereo matching method based on CUDA, and the IterRefine is the most up-to-date real-time stereo matching method in Middlebury database.

From table 2 we can see that since ESAW method is an AW based method with a simplification on aggregation process, it's not as effective as the AW method, which is consistent with the previous analysis. IterRefine method has conducted disparity refinement on the basis of ESAW, and has a better effect even than AW method. However, the proposed method is better than IterRefine, bringing the highest accuracy among all real-time stereo matching methods, and its average error rate is equivalent to that of SemiGlob method, with nearly 1 point lower than AW method and 30% higher than that of ESAW method. This should be mainly attributed to the accurate computation results in occlusion and complex texture regions.

In terms of execution time evaluation, the proposed method is mainly compared with ESAW method, which is widely recognized as a good algorithm of real time. Besides, the proposed method is an improved method based on ESAW. Table 3 provides the average execution time of the two methods on four Middlebury evaluating sequences, which is the total time of estimating two disparity maps for both left and right views. It can be seen that the proposed method, having a procedure of disparity refinement which ESAM does not have, is slower than ESAW. The speed of processing for Tsukuba by proposed method can reach nearly 20fps. But for images with larger resolution ratio and more disparity hypothesis levels, the proposed method cannot meet the real-time requirements. However, it's worth mentioning that the algorithm's execution time is closely related to the performance of GPU and the degree of parallel optimization. Considering the good parallel potential of proposed method, if using a GPU with more CUDA cores and larger memory, or conducting more in-depth parallel optimization according to the architecture, the execution time of the algorithm will be markedly improved.

Table 2. Quantitative results on the Middlebury datasets. / %.

Algorithm	Avg. % Bad Pixels	Tsukuba			Venus			Teddy			Cones
		nonocc	all	disc	nonocc	all	disc	nonocc	all	disc	nonocc	all	disc
Proposed	5.69	1.66	2.04	8.82	0.42	0.84	3.10	5.36	10.7	14.7	2.98	9.26	8.40
SemiGlob	5.76	2.61	3.29	9.89	0.25	0.57	3.24	5.14	11.8	13.0	2.77	8.35	8.20
AW	6.67	1.38	1.85	6.90	0.71	1.19	6.13	7.88	13.3	18.6	3.97	9.79	8.26
IterRefine	6.20	1.45	1.99	7.59	0.40	0.81	3.38	7.65	13.3	16.2	3.48	9.34	8.81
VariableWnd	7.60	1.99	2.65	6.77	0.62	0.96	3.20	9.75	15.1	18.2	6.28	12.7	12.9
ESAW	8.21	1.92	2.45	9.66	1.03	1.65	6.89	8.48	14.2	18.7	6.56	12.7	14.4

Table 3. Execution time (ms) for proposed algorithm and ESAW.

Algorithm	Tsukuba	Venus	Teddy	Cones
	384x288, 11 disp. levels	434x383, 16 disp. levels	450x375, 44 disp. levels	450x375, 44 disp. levels
Proposed	53.7	114.8	219.1	232.6
ESAW	34.8	75.3	174.3	202.4

6. Conclusion

This paper proposes a real-time stereo matching method based on adaptive window disparity refinement. The main features of this method include: 1) in association with the advantage of AD and Census transform, the proposed algorithm possesses a better adaptability to the variations of the image's intensity distortion; 2) in the stage of disparity refinement, based on the assumption that areas with similar colors should have similar disparity values, an adaptive window is built for each error point, and the occlusion error and mismatch error are refined respectively according to statistics of disparity values in the adaptive window, so as to enable the algorithm to have better estimation results in areas with discontinuous depths; 3) the algorithm enjoys a high degree of parallelization, and after parallel optimization, it can reach real-time process for Tsukuba images, and compared to the existing real-time stereo matching methods listed on the Middlebury evaluation platform, the proposed method is the most accurate one. Nevertheless, there is still a long distance to go to apply this algorithm in actual environment, and the next step is to conduct further parallel optimization for the algorithm to implement real-time process on the mainstream format images. In addition, there are too many parameters in proposed method, and the use of adaptive parameter mechanism is also worth researching.

Acknowledgements

This project is supported by the National Science and Technology major project "emergency maintenance equipment and technology for deep water" (No.2011ZX05027-005). The authors are also particularly grateful to the support from the R&D Centre of STMicroelectronics in Singapore.

References